 国家公务员考试信息汇总|2019国考Q群272771945|微信号sagwyks|国考课程
国家公务员考试信息汇总|2019国考Q群272771945|微信号sagwyks|国考课程
【导语】为了帮助广大考生有效地备战2019国家公务员考试,陕西公务员考试网汇总了国家公务员备考资料以及备考技巧等,供大家学习参考。祝各位考生备考顺利,一举成公!
在各类型的考试中数量关系是考生比较头疼的一部分,题型多样,过程耗时,其实这里的关键就是大家还没有掌握我们不同题型的巧妙求解方法,更多的是惯性思维,采用传统的方式列方程等进行求解。其实在数量关系环节特别讲究的是思维的活跃性方法的灵活性,而本节主要是结合极值问题中的和定最值问题,进行下讲解。中公教育专家将和大家一起研究下极值问题——和定最值问题的求解。
一、具体例题
例1.21个三好学生名额分给5个班级,且互不相等,问分得名额最多的班最多分多少?
例2.20个三好学生名额分给5个班级,且互不相等,问分得名额最多的班级最少分多少?若有21个呢?
例3.21个三好学生名额分给6个班级,且互不相等,问分得名额最多的班级最少分多少个?若有24个呢?若有25个呢?
二、题型介绍
这三个例题均属于和定最值问题。那具体如何判定呢?
和定最值:几个数的和一定,求其中某项量的最大或最小值。
解题原则:由于和是定值,若使其中某项最大,则其它项应该尽可能的小;
若使其中某项最小,则其他项应该尽可能的大。
三、例题解析
例1.求分得名额最多的班级最多分多少个,即求最大项的最大值。若使其尽可能多,则其他班级分得的数量应该尽可能少;但是条件中要求每人都有且互不等,所以至少也应该有1个,互不相等即从1开始的连续自然数,分别有1、2、3、4个。此时已经分出10个名额,还剩11个,都给剩下的班级,则分得名额最多的班级最多得11个名额。
例2.求分的名额最多的班级最少分多少,要想使其最少,则其它班级分得名额应该尽可能多,最大项尽可能小,其他项尽可能多,那么这是一个等均接近的过程。而最等均接近的时候是均分,即为20÷5=4,而题目中要求互不相等,所以此时为连续的自然数,且中间项为4,即为

则此时,分得名额最多的班级至少分得6个名额。
若有21个名额,即为21÷5=4……1,所以均分之后我们得到了中间值是4,而题目中要求互不相等,所以比4多的依次是拿到5、6个,比4少的依次拿到3、2个,构造出了数列:

此时还剩下一个名额,要想让分得名额最多的人班级拿到的尽可能少,这个名额应该考虑给拿的少的人,但是不管给拿到2、3、4、5个中的哪一个,都会出现和其他人相等的情况,不满足“互不相等”,所以6+1,分得名额最多的班级至少分7个。
例3.求分的名额最多的班级最少分多少,要想使其最少,则其它班级分得名额应该尽可能多,最大项尽可能小,其他项尽可能多,那么这是一个等均接近的过程。而最等均接近的时候是均分,即为21÷6=3.5,而题目中要求互不相等,且名额数应该为整数,则此时构造数列为,

此时,分得名额最多的班级至少分得6个名额。
若有24个名额,即为24÷6=4,所以均分之后我们得到了中间值是4,而题目中要求互不相等,所以构造出了数列:

则此时,分得名额最多的班级至少分得7个名额。
若有24个名额,即为25÷6=4余1,所以均分之后我们得到了中间值是4,而题目中要求互不相等,所以构造出了数列:
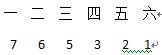
此时还剩下一个名额,要想让分得名额最多的人班级拿到的尽可能少,这个名额应该考虑给拿的少的人,所以给第四个人3+1=4,则分得名额最多的班级至少分7个。
上述几种情况是我们在和定最值问题中会遇到的情况,相比运用方程法求解,直接构造数列相对要直观简单许多,中公教育希望广大考生做题过程中勤于总结,掌握技巧性方法,节约时间,提高效率。
>> 推荐阅读| 2019国家公务员考试备考指导汇总 | |||
| 招考信息 | 时事政治 | 免费讲座 | 国考课程 |
| 行测备考 | 申论备考 | 行测题库 | 申论题库 |
责任编辑(刘露露)